Three point estimation

Per introdurre questo metodo di stima di progetto è d’obbligo anzitutto riportare la definizione del Practice Standard for Project Estimating del PMI:

Three-Point Estimating: tecnica utilizzata per stimare i costi o la durata applicando una media o una media pesata della stima ottimistica/pessimistica/verosimile, quando sussiste incertezza sulle singole stime delle attività. Questi metodi sono a volte descritti come una sottocategoria indipendente delle tecniche di stima (ad es. PMBOK Guide, Sezione 6.4.2. e 7.2.2.5). In ogni caso, l’utilizzo piuù comune è come metodo statistico, applicabile a qualsiasi tecnica di stima quantitativa per riflettere l’incertezza intrinseca dei dati disponibili, più comunemente nella stima per analogia. Un esempio della three-point estimation sarebbe la distribuzione triangolare rappresentata dalla formula E=(O+ML+P)/3, dove:

E = stima
O = Stima Ottimistica
ML = Stima più verosimile (Most Likely)
P = Stima Pessimistica

Cerchiamo di capire meglio di che si tratta e come si utilizza questa tecnica in Project Management.

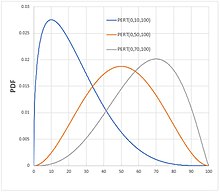
Anzitutto dobbiamo tenere presente che quando applichiamo questa tecnica stiamo assumendo implicitamente che le informazioni a nostra disposizione sono governati da una distribuzione di tipo PERT (vedi figura).

In probabilità e statistica, la distribuzione PERT è appunto una famiglia di distribuzioni di probabilità continue definite dai valori minimo (a), molto probabile (b) e massimo (c) che una variabile può assumere. È una trasformazione della distribuzione Beta a quattro parametri con un’ulteriore assunzione che il suo valore atteso sia:

\begin{aligned}
\mu &= \frac{a+4b+c}{4}
\end{aligned}

Quindi questa distribuzione media è definita come una media ponderata del minimo, del massimo e del valore più verosimile, considerando il valore più probabile dandogli un perso 4 volte maggiore.

E’ chiaro che sta alla sensibilità di chi compie l’analisi giudicare se l’assunzione fatta ha senso. Infatti spesso invece che la distribuzione PERT si utilizza la semplice distribuzione triangolare:

\begin{aligned}
\mu &= \frac{a+b+c}{3}
\end{aligned}

La distribuzione PERT (distribuzione beta) è caratterizzata da una curva più morbida rispetto a quella triangolare (che assegna un peso per i valori estremi uguale a quello del valore più verosimile, il ché la rende meno affidabile):

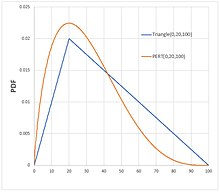
Nell’utilizzo della media pesata PERT, si affianca la deviazione standard σ:

\begin{aligned}
\sigma &= \frac{b-a}{6}
\end{aligned}

La deviazione standard è utile come concetto perché misura la variabilità (l’incertezza) della stima.

Ma come viene utilizzato tutto ciò dal Project Manager?

• Anzitutto deve produrre la Work Breakdown Structure (WBS), ovvero la decomposizione delle attività di progetto in task a cui è possibile assegnare una stima.
• Fatto questo, deve procedere alla stima del valore atteso e della deviazione standard, calcolandole come precedentemente esposto (sceglendo il tipo di distribuzione più opportuna).
• A questo punto deve procedere al calcolo del valore atteso totale mediante la formula:

\begin{aligned}
M_{progetto} &= \sum{\mu_{task}}
\end{aligned}

La deviazione standard dovrà calcolarla come segue:

\begin{aligned}
\sigma_{progetto} &=\sqrt{\sigma_{task}^2}
\end{aligned}

Il valore atteso e la deviazione standard così ricavati, vengono utilizzati per convertire le stime del tempo di progetto in intervalli di confidenza come segue:

• L’intervallo di confidenza del 68% per il tempo di lavoro reale del progetto è approssimativamente:

\begin{aligned}
M_{progetto} ± \sigma_{progetto}
\end{aligned}

• L’intervallo di confidenza del 90% per il tempo di lavoro reale del progetto è approssimativamente:

\begin{aligned}
M_{progetto} ± 1.645 \cdot \sigma_{progetto}
\end{aligned}

• L’intervallo di confidenza del 95% per il tempo di lavoro reale del progetto è approssimativamente:

\begin{aligned}
M_{progetto} ± 2 \cdot \sigma_{progetto}
\end{aligned}

• L’intervallo di confidenza del 99.7% per il tempo di lavoro reale del progetto è approssimativamente:

\begin{aligned}
M_{progetto} ± 3 \cdot \sigma_{progetto}
\end{aligned}

Generalmente nell’ambito della stima di progetti software (sistemi informativi), l’intervallo di confidenza utilizzato è il 95% per la stima di tutti i task e dei progetti.

Queste stime dell’intervallo di confidenza presuppongono che i dati di tutte le attività si combinino per essere approssimativamente normali (vedi normalità asintotica). In genere, affinché questa assunzione sia ragionevole, devono esserci circa 20-30 attività e ciascuna delle stime del valore atteso per le singole attività deve essere quanto più posssibile imparziale. In questo senso è bene sottolineare che devono essere gli esperti delle specifiche attività del progetto, che basandosi sulle proprie esperienze e conoscenze, effettuano la stima dei tre valori menzionati.

Come visto, l’incertezza sulle attività di progetto è espressa dalla varianza. E’ bene mettere in evidenza il fatto che le attività che presentano incertezza maggiore, ovvero varianza maggiore, sono quelle che presentano maggiori rischi. Per esse occorre quindi:

• identificare i rischi
• effettuare le dovute analisi
• sviluppare le risposte più opportune

Siamo di nuovo di fronte quindi ad una evidenza dell’opportunità di condurre in modo efficace e ben pianificato una opportuna gestioen dei rischi (risk management).

Esempio

Facciamo un breve esempio di applicazione della tecnica.

Supponiamo di avere un’attività A, per cui sia siano stati attribuiti i seguenti valori della stima della durata:

• valore ottimistico: 3 ore
• valore pessimistico: 12 ore
• valore verosimile: 9 ore

La distribuzione triangolare dà luogo al seguente valore atteso:

\begin{aligned}
\mu_{triangolare} &= \frac{3+9+12}{3} &= 8 h
\end{aligned}

La distribuzione PERT dà invece luogo al seguente valore atteso:

\begin{aligned}
\mu_{PERT} &= \frac{3+4 \cdot 9 + 12}{6} &= 8.5 h
\end{aligned}

La deviazione standard è data da:

\begin{aligned}
\sigma &= \frac{12-3}{6} &=1.5h
\end{aligned}

In questo caso, nell’ipotesi di utilizzo di una distribuzione normale con un intervallo di confidenza del 68%, avremo il 68% di probabilità che la durata dell’attività cada nell’intorno della media per un intervallo di ampiezza pari alla deviazione standard (8.5 ± 1.5), ovvero che si abbia la probabilità del 68% che la durata dell’attività A sia compresa tra 7 e 10 ore.

Fonti:

• Wikipedia
• 3-Points Estimating – Project Management.com