PERT – Project Evaluation Review Technique
Il PERT è un metodo statistico per la stima delle attività di progetto, che può essere applicato anche ai costi. E’ anche detto stima a tre valori (three point estimation), perché invece di affidarsi ad una semplice stima a valore singolo, fa capo alla determinazione dei valori di stima ottimale, probabile e pessimistica che risultano essere più adeguati per valutare tempi e costi di attività di progetto che presentano incertezza o complessità.
Il cuore del metodo consiste quindi nel coinvolgere i Subject-Matter Expert (SME) delle attività di progetto nel calcolo dei tre valori:
- tm: durata probabile
- to: durata ottimistica
- tp: durata pessimistica
Nel metodo PERT l’assunzione fondamentale è che le durate delle attività sono variabili aleatorie con distribuzione di tipo beta (distribuzione di probabilità di tipo beta), la cui deviazione standard è data da:
\begin{aligned} \sigma &= \frac{t_p-t_o}{6} \end{aligned}Una buona stima della durata media ponderata è data da:
\begin{aligned} t_e &= \frac{t_o+4t_m+t_p}{6} \end{aligned}Quindi nel metodo PERT, la durata più attendibile del progetto è data da te.
essendo la durata una variabile aleatoria, occorre indicare accanto a questo valore medio la varianza, che sarà data da:
\begin{aligned} \sigma^2 &= (\frac{t_p-t_o}{6})^2 \end{aligned}Questa varianza misura il grado di incertezza della durata prevista della singola attività.
La durata totale attesa (durata media) di progetto sarà la somma delle durate medie te di tutte le attività sul cammino critico:
\begin{aligned} D_T &= \sum_{i=1}^{n} t_{e_i} \end{aligned}dove tei è la durata media dell’attività i-esima e n è il numero delle attività che appartengono al cammino critico.
La varianza totale di progetto sarà data dalla somma delle varianze delle attività critiche:
\begin{aligned} \sigma_T^2 &= \sum_{i=1}^{n}\sigma_i^2 \end{aligned}L’intervallo di durata del progetto sarà:
\begin{aligned} RD_T &= [D_t \pm \sigma] \end{aligned}Accuratezza della stima
Informazione molto importante da determinare a questo punto è l’attendibilità teorica Z (ovvero la probabilità teorica) dell’intervallo RDT, che è data da:
\begin{aligned} Z &= \frac{(x-D_T)}{\sigma} \end{aligned}Se ad esempio vogliamo calcolare l’attendibilità teorica che una durata ipotizzata Di sia 
\begin{aligned} Z &= \frac{D_i-70}{\sigma} \end{aligned}La probabilità P che Z calcolato da questa formula abbia il valore 
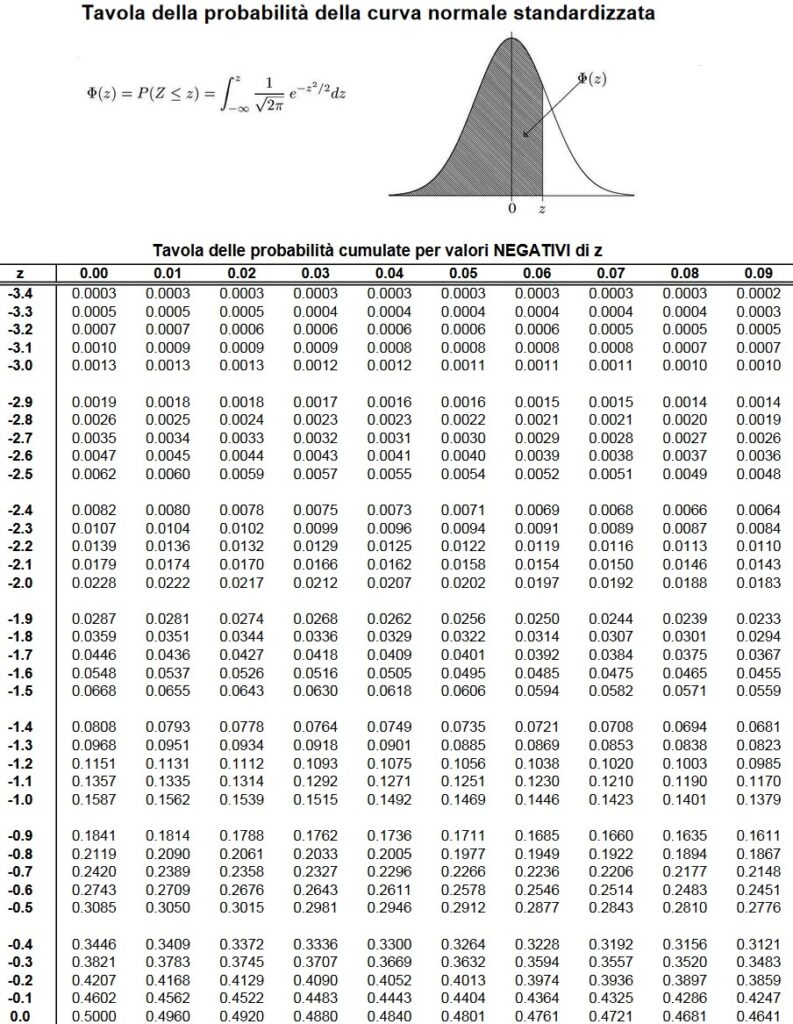
Se ad esempio dai coalcoli si ricava un valore:
\begin{aligned} P(D_i\le70) &= P(Z\le-0.79) &= 0.2148 \end{aligned}significherà che esiste una probabilità del 21.48% che la durata totale del progetto non superi 70 giorni (supponendo che l’unità di misura siano i giorni).
Fonti:
- Wikipedia: PERT/CPM
Immagini:
